Cho $\Large z_1, z_2$ là hai số phức thỏa mãn $\Large |z_1+1|=|z_1+i|$

Cho $\Large z_1, z_2$ là hai số phức thỏa mãn $\Large |z_1+1|=|z_1+i|$, $\Large |z_2-1-2i|=|z_2-2+i|$ và $\Large |z_1-z_2|=3\sqrt{2}$. Khi $\Large |z_2|$ đạt giá trị lớn nhất thì $\Large |z_1|$ bằng

• A. $\Large |z_1|=6\sqrt{2}$.
• B. $\Large |z_1|=3\sqrt{2}$.
• C. $\Large |z_1|=9\sqrt{2}$.
• D. $\Large |z_1|=4\sqrt{2}$.

Chọn A

Đặt $\Large z_1=x_1+y_1i$, $\Large z_2=x_2+y_2i$

$\Large \left\{\begin{align} & |z_1+1|=|z_1+i|\\ & |z_2-1-2i|=|z_2-2+i|\end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & |x_1+1+y_1i|=|x_1+y_1+1i|\\ & |x_2-1+y_2-2i|=|x_2-2+y_2+1i|\end{align}\right.$

$\Large \Leftrightarrow \left\{\begin{align} & x_1+1^2+y_1^2=x_1^2+y_1+1^2 \\ & x_2-1^2+y_2-2^2=x_2-2^2+y_2+1^2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & 2x_1=2y_1\\ & 2x_2=6y_2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x_1=y_1\\ & x_2=3y_2 \end{align}\right.$

Suy ra tập hợp điểm biểu diễn số phức $\Large z_1$ là đường thẳng $\Large d_1: x-y=0$, tập hợp điểm biểu diễn số phức $\Large z_2$ là đường thẳng $\Large d_2: x-3y=0$.

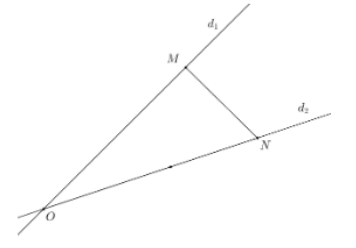
Gọi $\Large M, N$ lần lượt là điểm biểu diễn của số phức $\Large z_1, z_2$, do $\Large |z_1-z_2|=3\sqrt{2}\Leftrightarrow MN=3\sqrt{2}$.

Ta có $\Large \cos (d_1, d_2)=\dfrac{|1.1+(-1).(-3)|}{\sqrt{2}.\sqrt{10}}=\dfrac{2\sqrt{5}}{5}$ $\Large \Rightarrow \sin (d_1, d_2)=\dfrac{\sqrt{5}}{5}$ $\Large \Leftrightarrow \sin MON=\dfrac{\sqrt{5}}{5}$.

Xét $\Large \Delta OMN$ có $\Large \dfrac{MN}{\sin MON}=\dfrac{ON}{\sin OMN}$ $\Large \Leftrightarrow ON=\dfrac{3\sqrt{2}}{\dfrac{\sqrt{5}}{5}}.\sin OMN\leq 3\sqrt{10}$ hay $\Large |z_2|\leq 3\sqrt{2}$.

Do đó $\Large |z_2|$ đạt giá trị lớn nhất khi $\Large \Delta OMN$ vuông tại $\Large M\Rightarrow OM=\sqrt{ON^2-MN^2}=6\sqrt{2}$.

Vậy $\Large |z_1|=OM=6\sqrt{2}$.