Cho x,y thỏa mãn $\Large 3^{x+1+\dfrac{1}{4x}}-\mathrm{log}_
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho x,y thỏa mãn 3x+1+14x−log2[510−(y−2)√y+1]=0 với x>0. Giá trị của biểu thức P=4x2−28y2+6x2y+2020 là:
Đáp án án đúng là: D
Lời giải chi tiết:
Chọn D
Xét 3x+1+14x=log2[510−(y−2)√y+1]
Ta thấy 3x+14x+1≥32.√x.14x+1=9 ⇔x=12 (1)
Ta có 510−(y−2)√y+1=510−(y+1−3)√y+1 =510+3√y+1−√(y+1)3
Đặt √y+1=t(t≥0)
Xét f(t)=510+3t−t3
f′(t)=−3t2+3
f′(t)=0 ⇒[t=−1∉[0;+∞]t=1∈[0;+∞]
Ta có bảng biến thiên sau:
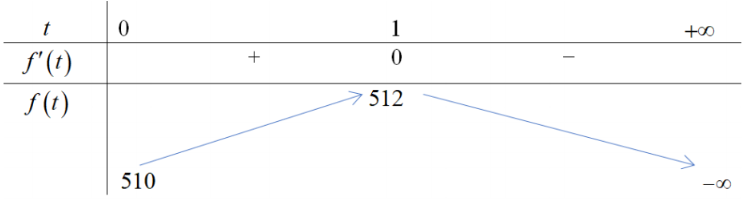
max[0;+∞]f(t)=f(1)=512
⇒log2[510−(y−2)√y+1]≤log2512=9 (2)
Từ (1) và (2) ⇒ ta có VT≥9,VP≤9
Dấu "=" xảy ra ⇔{x=12√y+1=1 ⇒{x=12y=0
Thay x,y vào P=4.(12)2+28.0+26.(12)2.0+2020=2021
Xem thêm các bài tiếp theo bên dưới