Cho tứ diện đều $\Large ABCD$ cạnh $\Large a,$ gọi $\Large O$ là tâm đ

Cho tứ diện đều $\Large ABCD$ cạnh $\Large a,$ gọi $\Large O$ là tâm đường tròn ngoại tiếp tam giác $\Large BCD.$ Khoảng cách từ $\Large O$ đến mặt phẳng $\Large (ABC)$ là

• A.

  A. $\Large \dfrac{a\sqrt{6}}{9}.$

• B.

  B. $\Large \dfrac{a\sqrt{6}}{6}.$

• C.

  C. $\Large \dfrac{a\sqrt{6}}{3}.$

• D.

  D. $\Large \dfrac{2a\sqrt{3}}{3}.$

Chọn A

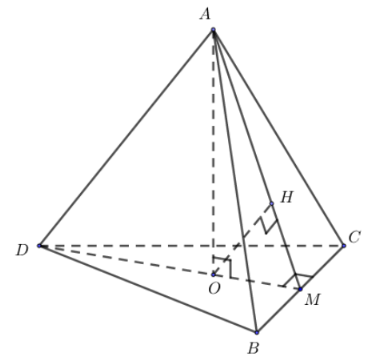
Gọi $\Large O$ là trọng tâm tam giác $\Large BCD$

Vì $\Large \Delta BCD$ đều nên $\Large O$ là tâm đường tròn ngoại tiếp tam giác $\Large BCD.$

Mặt khác $\Large ABCD$ là tứ diện đều nên $\Large AO\perp (BCD).$

Gọi $\Large M$ là trung điểm của $\Large BC$ $\Large \Rightarrow BC \perp DM$

Mà $\Large BC \perp AO \Rightarrow BC \perp (AOM)$ 

Lại có $\Large BC \subset (ABC) \Rightarrow (AOM) \perp (ABC).$

Trong tam giác $\Large AOM,$ kẻ $\Large OH \perp AM$

Ta có $\Large \left\{\begin{align} & (AOM) \perp (ABC) \\ & (AOM) \cap (ABC)=AM \\ & OH \subset (AOM) \\ & OH \perp AM \end{align}\right.$ $\Large \Rightarrow OH \perp (ABC) \Rightarrow d\big(O, (ABC)\big)=OH.$

Tam giác $\Large AOM$ vuông tại $\Large O,$ có $\Large OM=\dfrac{1}{3}DM=\dfrac{a\sqrt{3}}{6},$ $\Large OA=\sqrt{AD^2-OD^2}=\dfrac{a\sqrt{6}}{3}$

Suy ra $\Large OH=\dfrac{OM.OA}{\sqrt{OM^2+OA^2}}$ $\Large =\dfrac{\dfrac{a\sqrt{3}}{6}.\dfrac{a\sqrt{6}}{3}}{\sqrt{\bigg(\dfrac{a\sqrt{3}}{6}\bigg)^2+\bigg(\dfrac{a\sqrt{6}}{3}\bigg)^2}}$ $\Large =\dfrac{a\sqrt{6}}{9}.$

Vậy $\Large d\big(O, (ABC)\big)=\dfrac{a\sqrt{6}}{9}.$