Cho hàm số $\Large y=f(x)=\dfrac{ax+b}{cx+d},$ $\Large (a, b, c, d \in

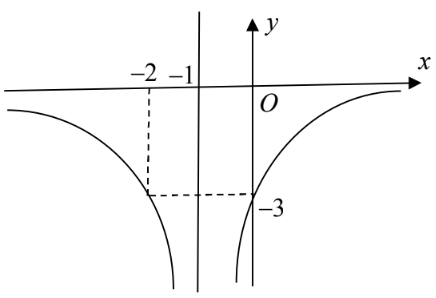
Cho hàm số $\Large y=f(x)=\dfrac{ax+b}{cx+d},$ $\Large (a, b, c, d \in \mathbb{R}, c \neq 0, d \neq 0, ad-bc \neq 0)$ có đồ thị là $\Large (C).$ Biết đồ thị hàm số $\Large y=f'(x)$ như hình vẽ và đồ thị $\Large (C)$ cắt trục tung tại điểm có tung độ bằng $\Large 2.$ Tiếp tuyến của $\Large (C)$ tại giao điểm của $\Large (C)$ với trục hoành có phương trình là:

• A.

  A. $\Large x+3y+2=0.$

• B.

  B. $\Large x-3y-2=0.$

• C.

  C. $\Large x-3y+2=0.$

• D.

  D. $\Large x+3y-2=0.$

Chọn D

Vì hàm số cắt $\Large Oy$ tại điểm có tung độ là $\Large 2$ nên suy ra $\Large \dfrac{b}{d}=2 \Rightarrow b=2d$

Ta có: $\Large {y}'=\dfrac{ad-bc}{(cx+d)^2}.$

Tiệm cận đứng: $\Large x=-1 \Rightarrow \dfrac{-d}{c}=-1 \Leftrightarrow c=d.$

Vì đồ thị hàm số $\Large y'$ đi qua điểm có tọa độ $\Large (0; -3)$ nên suy ra $\Large \dfrac{ad-bc}{d^2}=-3$

Thay $\Large b=2d; c=d$ vào ta suy ra $\Large a=-d.$

Khi đó ta có: $\Large f(x)=\dfrac{-dx+2d}{dx+d}=\dfrac{-x+2}{x+1}$

$\Large \Rightarrow (C) \cap Ox = (2; 0)$

$\Large f'(x)=\dfrac{-3}{(x+1)^2}$

Phương trình tiếp tuyến của hàm số $\Large y=f(x)$ với trục hoành là: $\Large y=f'(2)(x-2)+0=-\dfrac{1}{3}x+\dfrac{2}{3}$ $\Large \Leftrightarrow x+3y-2=0.$