Cho (H) là hình phẳng giới hạn bởi $\Large ( C ): y = \sqrt {
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
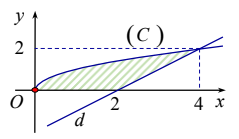
Cho (H) là hình phẳng giới hạn bởi (C):y=√x, d:y=x−2 và trục hoành (hình vẽ). Diện tích của (H) bằng

Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
Hoành độ giao điểm của (C) và trục hoành là 0.
Hoành độ giao điểm của đường thẳng d:y=x−2 và trục hoành là 2.
Hoành độ giao điểm của (C) và đường thẳng d:y=x−2 là 4.
Diện tích hình phẳng giới hạn bởi (C):y=√x, y=x−2 và trục hoành là: S=S1+S2
Với S1 là diện tích hình phẳng giới hạn bởi (C):y=√x và trục hoành và đường x=0;x=2.
=> S1=∫20√xdx = 23x√x|20 = 232√2 = 4√23
Với S2 là diện tích hình phẳng giới hạn bởi (C):y=√x và các đường y=x−2;x=2;x=4.
=> S2=∫42(√x−x+2)dx = (23x√x−x22+2x|42 = 163−(4√23+2) = 103−4√23
Do đó, S=S1+S2=103.
Xem thêm các bài tiếp theo bên dưới