Cho hình chóp $\Large S.ABC$ có $\Large SA = SB = SC = 4$, $\Large AB

Cho hình chóp $\Large S.ABC$ có $\Large SA = SB = SC = 4$, $\Large AB = BC = CA = 3$. Tính thể tích của khối nón giới hạn bởi hình nón có đỉnh là $\Large S$ và đáy là đường tròn ngoại tiếp $\Large \Delta  ABC$.

• A.

  A. $\Large 3 \pi$

• B.

  B. $\Large 4 \pi$

• C.

  C. $\Large \sqrt{13} \pi$

• D.

  D. $\Large 2 \sqrt{2} \pi$

Chọn C

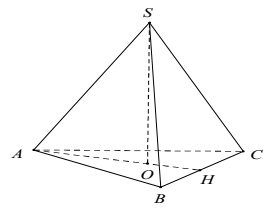
Từ giả thiết suy ra hình chóp $\Large S.ABC$ đều

$\Large \Rightarrow$ hình chiếu của đỉnh $\Large S$ trên $\Large mp(ABC)$ trùng với tâm $\Large O$ của đường tròn ngoại tiếp $\Large \Delta ABC$.

Bán kính đường tròn ngoại tiếp $\Large \Delta ABC$ là $\Large R = AO = \sqrt{3}$.

Chiều cao khối nón là: 

$\Large h = SO = \sqrt{SA^{2} - AO^{2}} =\sqrt{13}$.

Thể tích khối nón cần tìm là:

$\Large V = \dfrac{1}{3} \pi R^{2} h = \pi \sqrt{13}$.