Cho tứ diện $\Large S.ABC$ có $\Large SA = SB = SC = AB = AC = a; BC =

Cho tứ diện $\Large S.ABC$ có $\Large SA = SB = SC = AB = AC = a; BC = a \sqrt{2}$. Góc giữa hai đường thẳng $\Large AB$ và $\Large SC$ bằng:

• A.

  A. $\Large 120^{o}$

• B.

  B. $\Large 90^{o}$

• C.

  C. $\Large 0^{o}$

• D.

  D. $\Large 60^{o}$

Chọn D

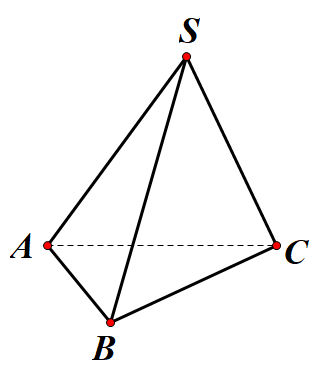
Do $\Large SA = SB = SC = AB = AC = a; BC = a \sqrt{2}$ suy ra hai tam giác $\Large SAB, SAC$ là các tam giác đều và tam giác $\Large SBC$ vuông cân tại $\Large S$.

Ta có:

$\Large \overrightarrow{SC} . \overrightarrow{AB} = \overrightarrow{SC}.(\overrightarrow{SB} - \overrightarrow{SA})$ 

$\Large = \overrightarrow{SC}. \overrightarrow{SB} - \overrightarrow{SC}.\overrightarrow{SA}= -a. a . cos 60^{o}= \dfrac{-a^{2}}{2}$

$\Large cos(\overrightarrow{SC}, \overrightarrow{AB}) = \dfrac{\overrightarrow{SC}. \overrightarrow{AB}}{SC . AB} = -\dfrac{1}{2}$

$ \Large \Rightarrow (\overrightarrow{SC}, \overrightarrow{AB}) = 120^{o}$

$\Large \Rightarrow (SC,AB) = 60^{o}$.