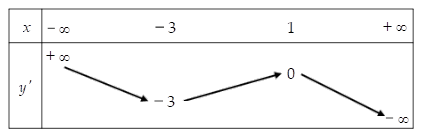
Cho hàm số $\Large y = f(x)$ có bảng biến thiên của đạo hàm $\Large y{

Cho hàm số $\Large y = f(x)$ có bảng biến thiên của đạo hàm $\Large y{}'$ như sau:

Bất phương trình $\Large f(x) < e^{x} + m$ đúng với mọi $\Large x \in (-1; 1)$ khi và chỉ khi

• A.

  A. $\Large m > f(-1) - \dfrac{1}{e}$.

• B.

  B. $\Large m > f(1) - e$.

• C.

  C. $\Large m \geq  f(1) - e$.

• D.

  D. $\Large m \geq  f(-1) - \dfrac{1}{e}$.

Chọn D

Theo bài ra ta có :

$\Large f(x) < e^{x} + m \Leftrightarrow  f(x) - e^{x} < m$ 

$\Large \Leftrightarrow m \geq \max_{\left [ -1; 1 \right ]} g(x)$

Xét $\Large g(x) = f(x) - e^{x}$, trên khoảng $\Large (-1; 1): \left\{\begin{matrix}f{}'(x) < 0 \\ e^{x} > 0\end{matrix}\right.$ 

$\Large \Rightarrow f{}'(x) - e^{x} < 0.$ Suy ra hàm số g(x) nghịch biến trên khoảng $\Large (-1;1)$

$\Large \Rightarrow \max_{\left [ -1; 1 \right ]}g(x) = g(-1) = f(-1)-\dfrac{1}{e}$

Vậy $\Large m \geq f(-1) - \dfrac{1}{e}$.