Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có

Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính $\Large R$ là:

 

• A.

  A. $\Large \dfrac {4R \sqrt{3}}{3}$

• B.

  B. $\Large R \sqrt{3}$

• C.

  C. $\Large \dfrac {R \sqrt{3}}{3}$

• D.

  D. $\Large \dfrac {2R \sqrt{3}}{3}$

Chọn D

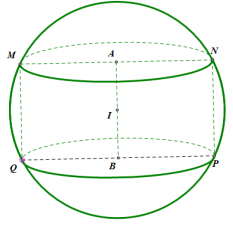
Giả sử hình cầu có tâm $\Large I$ và có bán kính là $\Large \mathbb {R}$, khối trụ có tâm của hai đáy là $\Large A, B$.

Gọi $\Large r, h$ là bán kính và chiều cao của khối trụ $\Large (0 < h = 2IA < 2R)$.

Ta có:

$\Large r = \sqrt {R^{2} - AI^{2}} = \sqrt {R^{2} - \dfrac{h^{2}}{4}}$.

Thể tích của khối trụ là:

$\Large V = \pi r^{2} h= \pi \left ( R^{2} - \dfrac{h^{2}}{4} \right )h$ 

$\Large = \pi\left ( R^{2}h - \dfrac{h^{3}}{4} \right )$

Xét hàm số $\Large f(h) = R^{2}h - \dfrac{h^{3}}{4}$ với $\Large 0 < h < 2R$.

Có: $\Large f{}'(h) = R^{2} - \dfrac{3}{4}h^{2}$

$\Large f{}'(h) = 0 \Leftrightarrow h = \dfrac{2\sqrt{3}}{3}R$

Ta có bảng biến thiên:

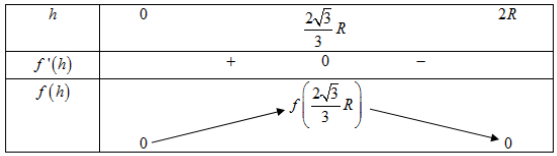
Dựa vào bảng biến thiên ta thấy thể tích của hình trụ lớn nhất khi và chỉ khi $\Large h = \dfrac{2\sqrt{3}}{3}R$.