Cho hình chóp S.ABCD có đáy là hình thang vuông tại $\Large A
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, SA⊥(ABCD). Góc giữa SB và mặt phẳng đáy bằng 45o, E là trung điểm của SD, AB=2a, AD=DC=a. Tính khoảng cách từ B đến (ACE).
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
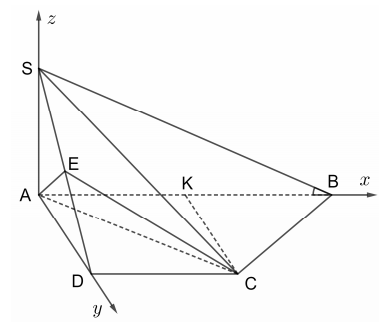
(^SB,(ABCD))=45o⇒^SBA=45o
=> Tam giác SAB vuông cân tại A
⇒SA=AB=2a.
Chọn hệ trục Axyz như hình vẽ. Ta được A(0;0;0), S(0;0;2a), B(2a;0;0), D(0;a;0).
Gọi K là trung điềm của AB. Nhận xét rằng tứ giác ADCK là hình chữ nhật.⇒C(a;a;0).
E là trung điểm của SD. E(0;a2;a).
[→AE,→AC]=(−a2;a2;−a22)=−a22(2;−2;1)
Mặt phẳng (ACE) đi qua A(0;0;0) và nhận vectơ (2;−2;1) là một vectơ pháp tuyến nên có phương trình 2x−2y+z=0.
Vậy khoảng cách từ B đến (ACE) là d(B,(ACE))=|2.2a|√22+(−2)2+12=4a3.