Cho hình lập phương $\Large ABCD.A{}'B{}'C{}'D{}'$ cạnh $\Large 2a$. G

Cho hình lập phương $\Large ABCD.A{}'B{}'C{}'D{}'$ cạnh $\Large 2a$. Gọi $\Large M$ là trung điểm của $\Large BB{}'$ và $\Large P$ thuộc cạnh  $\Large DD{}'$ sao cho  $\Large DP = \dfrac{1}{4}DD{}'$. Biết mặt phẳng  $\Large (AMP)$ cắt  $\Large CC{}'$ tại  $\Large N$, thể tích của khối đa diện  $\Large AMNPBCD$ bằng

• A.

  A.  $\Large \dfrac{9a^{3}}{4}$

• B.

  B.  $\Large 2a^{3}$

• C.

  C.  $\Large 3a^{3}$

• D.

  D.  $\Large \dfrac{11a^{3}}{3}$

Chọn C

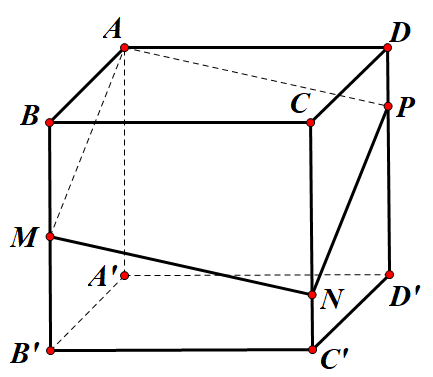
Thể tích khối lập phương là: $\Large V = 8a^{3}$

Ta có:

$\Large \dfrac{V_{AMNPBCD}}{V_{ABCD.A{}'B{}'C{}'D}}= \dfrac{1}{2}\left ( \dfrac{BM}{BB{}'}+\dfrac{DP}{DD{}'} \right )= \dfrac{1}{2}\left ( \dfrac{1}{2} + \dfrac{1}{4}\right )= \dfrac{3}{8}$

$\Large \Rightarrow V_{AMNPBCD} = \dfrac{3}{8}.V_{ABCD.A{}'B{}'C{}'D{}'} = 3a^{3}$.