Cho lăng trụ tam giác ABC.A’B’C’ có đáy là một tam giác vuông cân tại

Cho lăng trụ tam giác ABC.A’B’C’ có đáy là một tam giác vuông cân tại B, $\large AB= BC= a,\, AA’= a\sqrt{2}$, M và E lần lượt là trung điểm của BC và BB’. Tính khoảng cách giữa đường thẳng B’C và mặt phẳng (AME)

• A. $\large \dfrac{a}{\sqrt{7}}$
• B. $\large \dfrac{a\sqrt{3}}{2}$
• C. $\large \dfrac{2a}{\sqrt{5}}$
• D. $\large a\sqrt{3}$

Chọn A

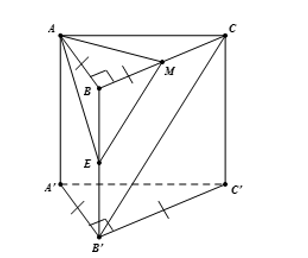
Ta có : $\large EM// B’C\Rightarrow  B’C//(AME)$
$\large \Rightarrow  d(B’C,(AME))= d(C, (AME))= d(B, (AME))$
Xét khối chóp BAME có các cạnh BE, AB, BM đôi một vuông góc với nhau nên 
$\large \dfrac{1}{d^2(B, (AME))}= \dfrac{1}{AB^2}+\dfrac{1}{MB^2}+ \dfrac{1}{EB^2}\Leftrightarrow \dfrac{1}{d^2(B, (AME))}= \dfrac{7}{a^2}$
$\large \Leftrightarrow d^2 (B,(AME))= \dfrac{a^2}{7}\Leftrightarrow d(B, (AME))= \dfrac{a}{\sqrt{7}}$