Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đ

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều. gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Biết $\large SH\perp (ABC)$, gọi $\large \varphi $ là góc giữa đường thẳng SA và mặt phẳng (SHK). Mệnh đề nào sau đây đúng?

• A. $\large \tan\varphi= \sqrt{7}$
• B. $\large \tan\varphi = \dfrac{\sqrt{2}}{4}$
• C. $\large \tan\varphi = \dfrac{\sqrt{7}}{7}$
• D. $\large \tan\varphi = \dfrac{\sqrt{14}}{4}$

Chọn C

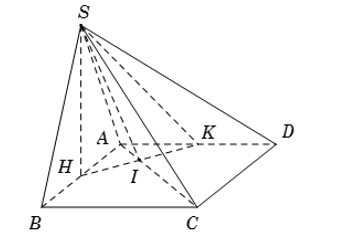
Gọi $\large I= HK\cap AC$. Do H, K lần lượt là trung điểm của AB và AD nên $\large HK//BD$. Suy ra: $\large HK\perp AC$
Lại có: $\large AC\perp SH$ nên suy ra $\large AC\perp (SHK)$
Do đó: $\large \angle (SA, (SHK))= \angle (SA, SI) = \angle ASI$
Tam giác SIA vuông tại I, có $\large \tan\widehat{ASI}= \dfrac{AI}{SI}= \dfrac{\dfrac{1}{4}.AC}{\sqrt{SA^2-AI^2}}= \dfrac{\sqrt{7}}{7}$