Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh $\large AB= 2,\, AD=3,

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh $\large AB= 2,\, AD=3,\, AA’=4$. Góc giữa hat mặt phẳng  (AB’D’) và (A’C’D) là $\large \alpha $. Tính giá trị gần đúng của góc $\large \alpha $

• A. $\large 45,2^\circ $
• B. $\large 38,1^\circ $
• C. $\large 53,4^\circ $
• D. $\large 61,6^\circ $

Chọn D

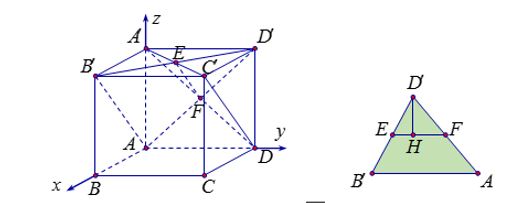
Cách 1: Hai mặt phẳng (AB’D’) và (A’C’D) có giao tuyến là EF như hình vẽ. Từ A’ và D’ ta kẻ hai đoạn vuông góc lên giao tuyến EF sẽ là chuyên một điểm H như hình vẽ. khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng A’H và D’H
Tam giác DEF lần lượt có $\large D’E= \dfrac{D’B’}{2}= \dfrac{\sqrt{13}}{2},\, D’F= \dfrac{D’A}{2}= \dfrac{5}{2},\, EF= \dfrac{B’A}{2}= \sqrt{5}$
Theo Hê-rông ta có: $\large S_{DEF}= \dfrac{\sqrt{61}}{4}$. Suy ra: $\large D’H=\dfrac{2S_{DEF}}{EF}= \dfrac{\sqrt{305}}{10}$
Tam giác D’A’H có $\large \cos\widehat{A’HD’}= \dfrac{H’A^2+HD’^2-A’D’^2}{2.HA’.HD’}=- \dfrac{29}{61}$
Do đó: $\large \widehat{A’HD’}= 118,4^\circ $ hay $\large \angle (A’H, D’H)\approx 180^\circ – 118,4^\circ = 61,6^\circ $