Cho lăng trụ đứng $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho lăng trụ đứng $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác vuông tại $\large B$ và $\large BA=BC=1$. Cạnh $\large A'B$ tạo với mặt đáy $\large (ABC)$ góc $\large 60^{\circ}$. Thể tích của khối lăng trụ đã cho bằng:
Đáp án án đúng là: C
Lời giải chi tiết:
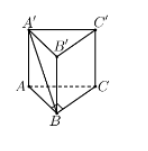
Xác định: $\large 60^{\circ}=\left ( \widehat{A'B,(ABC)} \right )=\left ( \widehat{A'B,AB} \right )=\widehat{A'BA}$
Tam giác vuông $\large A'AB$, ta có $\large AA'=AB\cdot \tan \widehat{A'BA}=\sqrt{3}$
Diện tích tam giác: $\large S_{ABC}=\frac{1}{2}BA.BC=\frac{1}{2}$
Vậy $\large V=S_{\bigtriangleup ABC}.AA'=\frac{\sqrt{3}}{2}$
Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$ có $\large AB=AA'=a$, đườ
- Cho hình trụ $\large ABCD.A'B'C'D'$ có tất cả các cạnh đều bằng $\larg
- Cho lăng trụ $\large ABCD.A'B'C'D'$ có đáy $\large ABCD$ là hình vuông
- Cho tứ diện $\large ABCD$ có thể tích bằng $\large 24$ và $\large G$ l
- Cho tứ diện $\large ABCD$ có $\large AB,AC,AD$ đôi một vuông góc và $\