Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc và $\
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=6a,AC=9a,AD=3a. Gọi M,N,P lần lượt là trọng tâm của các tam giác ABC,ACD,ADB. Thể tích của khối tứ diện AMNP bằng:
Đáp án án đúng là: A
Lời giải chi tiết:
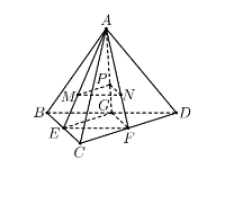
Ta có VABCD=16AB.AC.AD=27a3
Do S△EFG=14S△BCD→VAEFG=14VABCD=274a3
Ta có VA.MNPVA.EFG=AMAE.ANAF.APAG=23.23.23=827
→VA.MNP=827VA.EFG=2a3
Đáp án A
Xem thêm các bài tiếp theo bên dưới