Cho hình chóp S.ABCS.ABC có chiều cao bằng 9, diện tích đáy bằng 5
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCS.ABC có chiều cao bằng 9, diện tích đáy bằng 5. Gọi MM là trung điểm của cạnh SBSB và NN thuộc cạnh SCSC sao cho NS=2NCNS=2NC. Thể tích của khối chóp A.BMNCA.BMNC bằng:
Đáp án án đúng là: B
Lời giải chi tiết:
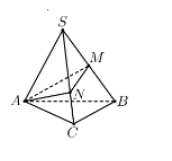
Từ giả thiết, ta có SNSC=23SNSC=23 và SMSB=12SMSB=12
Thể tích khối chóp VS.ABC=13⋅9⋅5=15VS.ABC=13⋅9⋅5=15
Ta có VS.AMNVS.ABC=SMSB.SNSC=13⇒VABMNC=23VS.ABC=10VS.AMNVS.ABC=SMSB.SNSC=13⇒VABMNC=23VS.ABC=10
Đáp án B