Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình bình hành.

Cho hình chóp $\large S.ABCD$ có đáy $\large ABCD$ là hình bình hành. Gọi $\large M,N$ lần lượt là trung điểm của các cạnh $\large AB,BC$. Điểm $\large I$ thuộc đoạn $\large SA$. Biết mặt phẳng $\large (MNI)$ chia khối chóp $\large S.ABCD$ thành hai phần, phần chứa đỉnh $\large S$ có thể tích bằng $\large\frac{7}{13}$ lần phần còn lại. Tính tỉ số $\large k=\frac{IA}{IS}$

• A.

  A. $\large\frac{1}{2}$

• B.

  B. $\large\frac{2}{3}$

• C.

  C. $\large\frac{1}{3}$

• D.

  D. $\large\frac{3}{4}$

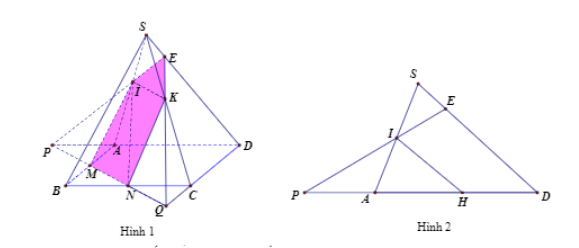
Mặt phẳng chứa $\large (MNI)$ cắt khối chóp theo thiết diện như hình 1. Đặt $\large V_{S.ABCD}=V$

Ta có $\large S_{\bigtriangleup ADM}=S_{\bigtriangleup BMN}=\frac{1}{4}S_{\bigtriangleup ABC}=\frac{1}{8}S_{ABCD}\Rightarrow \frac{S_{\bigtriangleup ADM}}{S_{ABCD}}=\frac{1}{8}$

$\large\frac{d(I,(ABCD))}{d(S,(ABCD))}=\frac{IA}{SA}=\frac{k}{k+1}$

$\large\Rightarrow \frac{V_{I.ADM}}{V_{S.ABCD}}=\frac{S_{\bigtriangleup ADM}}{S_{ABCD}}\cdot \frac{d(I,(ABCD))}{d(S.(ABCD))}=\frac{k}{8(k+1)}\Rightarrow V_{I.ADM}=\frac{k}{8(k+1)}V$

Do $\large MN//AC\Rightarrow IK//AC\Rightarrow IK//(ABCD)\Rightarrow d(I;(ABCD))=d(K;(ABCD))$

Mà $\large S_{\bigtriangleup ADM}=S_{\bigtriangleup NCQ}\Rightarrow V_{I.ADM}=V_{K.NCQ}=\frac{k}{8(k+1)}V$

Kẻ $\large IH//SD(H\in SD)$ như hình 2, ta có:

$\large\frac{IH}{SD}=\frac{AH}{AD}=\frac{AI}{AS}=\frac{k}{k+1}$

$\LARGE\frac{IH}{ED}=\frac{PH}{PD}=\frac{PA}{PD}+\frac{AH}{PD}=\frac{PA}{PD}+\frac{2AH}{3AD}=\frac{1}{3}+\frac{2k}{3(k+1)}=\frac{3k+1}{3(k+1)}$

$\LARGE\Rightarrow \frac{ED}{SD}=\frac{IH}{SD}:\frac{ID}{ED}=\frac{3k}{3k+1}\Rightarrow \frac{d(E,(ABCD))}{d(S,(ABCD))}=\frac{ED}{SD}=\frac{3k}{3k+1}$

$\large V_{EIKAMNCD}=\frac{13}{20}V\Leftrightarrow V_{E.PDC}-V_{I.APM}-V_{K.NQC}=\frac{13}{20}V$

$\large\Leftrightarrow \frac{27k}{8(3k+1)}V-\frac{k}{8(k+1)}V-\frac{k}{8(k+1)}V=\frac{13}{20}V$

$\large\Leftrightarrow \frac{27k}{2(3k+1)}-\frac{k}{k+1}=\frac{13}{5}\Leftrightarrow k=\frac{2}{3}$

Đáp án B