Cho hình chóp $\large S.ABCD$ có đáy là hình chữ nhật với $\large AB=4

Cho hình chóp $\large S.ABCD$ có đáy là hình chữ nhật với $\large AB=4, SC=6$. Tam giác $\large SAD$ cân tại $\large S$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích lớn nhất của khối chóp đã cho bằng:

• A.

  A. 40

• B.

  B. 80

• C.

  C. $\large\frac{40}{3}$

• D.

  D. $\large\frac{80}{3}$

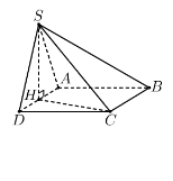
Gọi $\large H$ là trung điểm của $\large AD$. Từ giả thiết suy ra $\large SH\perp (ABCD)$

Đặt $\large AD=x$, suy ra $\large HC=\sqrt{\frac{x^{2}}{4}+16}$ và $\large SH=\sqrt{20-\frac{x^{2}}{4}}$

Điều kiện: $\large 0

Khi đó $\large V_{S.ABCD}=\frac{1}{3}S_{ABCD}.SH=\frac{1}{3}.4x\sqrt{20-\frac{x^{2}}{4}}=\frac{1}{3}\left ( 2x\sqrt{80-x^{2}} \right )\leq \frac{1}{3}\left ( x^{2} +80-x^{2}\right )=\frac{80}{3}$

Đáp án D