Cho hình chóp $\large S.ABC$ có đáy là tam giác vuông tại $\large A$ v

Cho hình chóp $\large S.ABC$ có đáy là tam giác vuông tại $\large A$ và $\large\widehat{ABC}=30^{\circ}$ . Đỉnh $\large S$ cách đều các điểm $\large A,B,C$. Biết khoảng cách từ $\large S$ đến mặt phẳng đáy bằng $\large a\sqrt{3}$ , khoảng cách từ $\large B$ đến mặt phẳng $\large (SAC)$ bằng $\large 2a\sqrt{2}$. Thể tích khối chóp đã cho bằng.

 

• A.

  A. $\large 2\sqrt{2}a^{3}$

• B.

  B. $\large 4a^{3}$

• C.

  C.  $\large 4\sqrt{2}a^{3}$

• D.

  D.  $\large 8a^{3}$

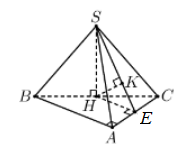
Gọi $\large H$ là trung điểm $\large BC$. Từ giả thiết suy ra $\large SH\perp (ABC)\rightarrow SH=a\sqrt{3}$

Ta có $\large d[B;(SAC)]=2d[H;(SAC)]\rightarrow d[H;(SAC)]=a\sqrt{2}$

Kẻ $\large HE\perp AC (E$ là trung điểm $\large AC)$, kẻ $\large HK\perp SE$ (1)

Ta có $\large\left\{\begin{align}AC\perp HE\\ AC\perp SH\end{align}\right.$ $\large\Rightarrow AC\perp (SHE)\Rightarrow AC\perp HK
$ (2)

Từ (1) và (2), suy ra $\large HK\perp (SAC)$ nên $\large HK=d[H;(SAC)]=a\sqrt{2}$

Trong tam giác vuông $\large SHE$, tính được $\large HE=\sqrt{6}a\Rightarrow AB=2\sqrt{6}a\xrightarrow{\widehat{ABC}=30^{\circ}}AC=2\sqrt{2}a$

Diện tích tam giác $\large S_{\bigtriangleup ABC}=\frac{1}{2}AB.AC=4\sqrt{3}a^{2}$

Vậy thể tích khối chóp $\large V_{S.ABC}=\frac{1}{3}S_{\bigtriangleup ABC}.SH=4a^{3}$

Đáp án B