Cho hình chóp $\large S.ABC$ có đáy là tam giác vuông cân tại $\large

Cho hình chóp $\large S.ABC$ có đáy là tam giác vuông cân tại $\large A$. Cạnh bên $\large SA$ vuông góc với mặt phẳng đáy, khoảng cách từ $\large A$ đến mặt phẳng $\large SBC$ bằng 3. Gọi $\large\alpha $ là góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABC)$, tính $\large\cos \alpha $ khi thể tích khối chóp $\large S.ABC$ nhỏ nhất

• A.

  A. $\large\cos \alpha =\frac{\sqrt{2}}{2}$

• B.

  B. $\large\cos \alpha =\frac{1}{3}$

• C.

  C. $\large\cos \alpha =\frac{\sqrt{3}}{3}$

• D.

  D. $\large\cos \alpha =\frac{2}{3}$

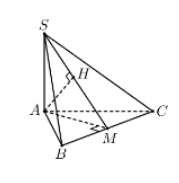
Đặt $\large AB=AC=x$, $\large SA=y$. Khi đó $\large V_{S.ABC}=\frac{1}{6}x^{2}y$

Vì $\large AB,AC,AS$ đôi một vuông góc nên

$\large\frac{1}{9}=\frac{1}{d^{2}(A,(SBC))}=\frac{1}{x^{2}}+\frac{1}{x^{2}}+\frac{1}{y^{2}}\geq 3\sqrt[3]{\frac{1}{x^{4}y^{2}}}$

Suy ra $\large x^{2}y\geq 81\sqrt{3}\rightarrow V_{S.ABC}=\frac{1}{6}x^{2}y\geq \frac{27\sqrt{3}}{2}$

Dấu "=" xảy ra $\large\Leftrightarrow x=y=3\sqrt{3}$

Khi đó $\large\cos \alpha=\cos\widehat{SMA}=\frac{\sqrt{3}}{3}$

Đáp án C