Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình

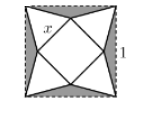
Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp như hình vẽ. Để thể tích khối chóp lớn nhất thì cạnh đáy $\large x$ của hình chóp bằng:

• A.

  A. $\large x=2\sqrt{2}$

• B.

  B. $\large x=\frac{\sqrt{2}}{5}$

• C.

  C. $\large x=\frac{2}{5}$

• D.

  D. $\large x=\frac{2\sqrt{2}}{5}$

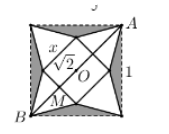
Ta có $\large BM=BO-MO=\frac{1}{2}AB-MO=\frac{\sqrt{2}}{2}-\frac{x}{2}$

Chiều cao của hình chóp:
$\large h=\sqrt{BM^{2}-MO^{2}}=\sqrt{\left ( \frac{\sqrt{2}}{2}-\frac{x}{2} \right )^{2}-\left ( \frac{x}{2} \right )^{2}}=\sqrt{\frac{1-x\sqrt{2}}{2}}$

Suy ra thể tích của khối chóp:

$\large V=\frac{1}{3}x^{2}\sqrt{\frac{1-x\sqrt{2}}{2}}=\frac{1}{3}\sqrt{\frac{x^{4}-x^{3}\sqrt{2}}{2}}$

Khảo sát $\large f(x)=x^{4}-x^{3}{\sqrt{2}}$ trên $\large\left ( 0;\frac{\sqrt{2}}{2} \right )$ được $\large f(x)$ lớn nhất khi $\large x=\frac{2\sqrt{2}}{5}$

Đáp án D