CHo hình chóp $\large S.ABC$ có đáy $\large ABC$ là tam giác đều và có

CHo hình chóp $\large S.ABC$ có đáy $\large ABC$ là tam giác đều và có $\large SA=SB=SC=1$. Thể tích lớn nhất của khối chóp đã cho bằng:

• A.

  A. $\large\frac{1}{6}$

• B.

  B. $\large\frac{1}{12}$

• C.

  C. $\large\frac{\sqrt{2}}{12}$

• D.

  D. $\large\frac{\sqrt{3}}{12}$

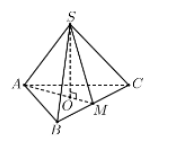
Gọi $\large O$ là tâm tam giác đều $\large ABC$.

Từ giả thiết suy ra $\large SO\perp (ABC)$

Đặt $\large AB=x$, suy ra $\large OA=\frac{x\sqrt{3}}{3}$ và $\large SO=\sqrt{1-\frac{x^{2}}{3}}$

Điều kiện $\large 0

Khi đó $\large V_{S.ABC}=\frac{1}{3}S_{\bigtriangleup ABC}.SO=\frac{1}{12}.x^{2}\sqrt{3-x^2}$

Xét hàm $\large f(x)=\frac{1}{12}x^{2}\sqrt{3-x^{2}}$ trên $\large (0;\sqrt{3})$, ta được $\large\underset{(0;\sqrt{3})}{max}f(x)=f(\sqrt{2})=\frac{1}{6}$

Đáp án A