Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh $\Large 2 a,

Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh $\Large 2 a, AA^{\prime}=a \sqrt{3}$ . Hình chiếu của A' lên mặt phẳng ABCD trùng với trung điểm I của AB. Gọi K là trung điểm BC. Tính khoảng cách từ điểm I đến mặt phẳng (A'KD).

• A. $\Large \dfrac{3 a \sqrt{2}}{19}$
• B. $\Large \dfrac{3 a \sqrt{38}}{19}$
• C. $\Large \dfrac{4 \sqrt{2} a}{3}$
• D. $\Large \dfrac{3 \sqrt{2} a}{8}$

Chọn B

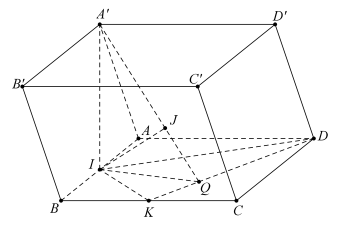
Gọi Q và J lần lượt là hình chiếu của I lên KD và A'Q , ta có $\Large I J \perp\left(A^{\prime} K D\right)$

Khi đó $\Large d\left(I ;\left(A^{\prime} K D\right)\right)=I J=\dfrac{A^{\prime} I . I Q}{\sqrt{A^{\prime} I^{2}+I Q^{2}}}$

$\Large I Q=\dfrac{2 S_{IK D}}{K D}=\dfrac{2\left(S_{A B C D}-S_{I A D}-S_{I K B}-S_{C K D}\right)}{\sqrt{C D^{2}+C K^{2}}}$$\Large =\dfrac{2\left(2 a \cdot 2 a-\dfrac{1}{2}. 2 a \cdot a-\dfrac{1}{2}. a \cdot a-\dfrac{1}{2}. 2 a \cdot a\right)}{\sqrt{(2 a)^{2}+a^{2}}}=\dfrac{3 a \sqrt{5}}{5}$

Vậy $\Large d\left(I ;\left(A^{\prime} K D\right)\right)=\dfrac{A^{\prime} I . I Q}{\sqrt{A^{\prime} I^{2}+I Q^{2}}}=\dfrac{3 a \sqrt{38}}{19}$