Cho lăng trụ ABC.A'B'C' có chiều cao bằng 8 và đáy là tam giác đều cạn

Cho lăng trụ ABC.A'B'C' có chiều cao bằng 8 và đáy là tam giác đều cạnh bằng 4. Gọi M, N, P lần lượt là tâm của các mặt bên (ABB'A'), (ACC'A'), (BCC'B'). Thể tích của khối đa diện lồi có các định là các điểm A, B, C, M, N, P bằng 

• A.

  $\large \dfrac{28\sqrt{3}}{3}$

• B.

  $\large 12\sqrt{3}$

• C.

  $\large 16\sqrt{3}$

• D.

  $\large \dfrac{40\sqrt{3}}{3}$

Chọn B

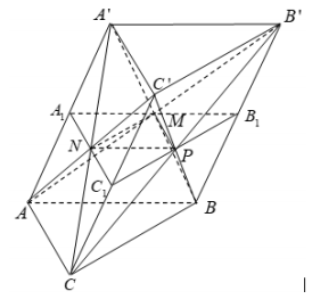
Gọi V là thể tích khối lăng trụ ABC.A'B'C'

Gọi $\large A_1,\, B_1,\, C_1$ lần lượt là trung điểm của AA', BB', CC'

Khi đó: $\large (A_1B_1C_1)//(ABC)//(A'B'C')$

Khi đó: $\large V_{ACBMNP}= V_{ABC.A_1B_1C_1}- V_{AA_1MN}- V_{BB_1MP} - V_{CC_1NP}$

Ta có: $\large V_{ABC.A_1B_1C_1} = \dfrac{1}{2}V_{ABC.A'B'C'}= \dfrac{1}{2}V$

$\large V_{AA_1MN} = \dfrac{1}{3}d(A; (A_1B_1C_1)).S_{A_1MN} = \dfrac{1}{3}.\dfrac{1}{2}.d((ABC); (A'B'C')) .\dfrac{1}{4}.S_{ABC} = \dfrac{1}{24}V$

Chứng minh tương tự ta có: $\large V_{BB_1MP } = V_{CC_1NP }= \dfrac{V}{24}$

$\large \Rightarrow V_{ABCMNP} = \dfrac{1}{2}V- \dfrac{3V}{24} = \dfrac{3V}{8}$

Ta có: $\large V=8.\dfrac{4^2\sqrt{3}}{4} = 32\sqrt{3}\Rightarrow V_{ABCMNP} = \dfrac{3.32\sqrt{3}}{8} = 12\sqrt{3}$