Cho khối nón có độ lớn góc ở đỉnh là π3π3. Một khố

MỤC LỤC
Câu hỏi:
Cho khối nón có độ lớn góc ở đỉnh là π3π3. Một khối cầu (S1)(S1) nội tiếp trong hình nón. Gọi S2S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1;S3S1;S3 là khối tiếp xúc với tất cả các đường sinh của nón với S1;....;SnS1;....;Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn−1Sn−1. Gọi V1,V2,V3,...,Vn−1,VnV1,V2,V3,...,Vn−1,Vn lần lượt là thể tích của khối cầu S1,S2,S3,...,Sn−1,SnS1,S2,S3,...,Sn−1,Sn và V là thể tích của khối nón. Tính giá trị của biểu thức T=limV1+V2+...+VnVT=limV1+V2+...+VnV.
Đáp án án đúng là: B
Lời giải chi tiết:
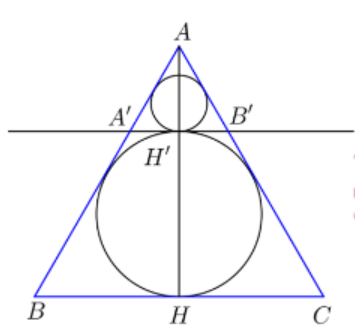
Chọn B
Thiết diện qua trục của hình nón là một tam giác đều cạnh l.
Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là r1=13.l√32=l√36r1=13.l√32=l√36
Áp dụng định lý Ta-lét ta được:
AA′AB=AH′AH=AH−HH′AH=l√32−l√33l√32=13
⇒AA′=l3.
Tương tự ta tìm được:
r2=l3.√36=l√318=r13;r3=r132,r4=r133,....,rn=r13n−1
V1=43πr31,V2=43πr32=43π(r13)3=133V1,
V3=1(33)2V1,...,Vn=1(33)n−1V1
Khi đó:
T=limV1+V2+...+VnV=limV1(1+133+1(33)2+...+1(33)n−1)V=limV1.SV
Đặt S=1+133+1(33)2+...+1(33)n−1.
Đây là tổng CSN lùi vô hạn với công bội
q=133<1⇒limS=11−133=2726
V1+V2+...+Vn=2726.V1=2726.43π(l√36)3=√352πl3
V=13πr2h=13π(12)2.l√32=√3πl324⇒T=√352πl3√3πl324=613
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên $\lar
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô
- Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc $\large \wi
- Cho tứ diện ABCD có DA vuông góc với mp( ABC ), DB⊥BC ,