Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a. Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng $\large 45^{\circ}$. Gọi N là trung điểm SA, h là chiều cao của khối chóp S.ABCD và R là bán kính mặt cầu ngoại tiếp khối chóp N.ABC. Biểu thức liên hệ giữa R và h là:
Đáp án án đúng là: A
Lời giải chi tiết:
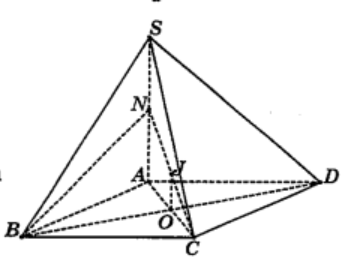
Ta có $\large 45^{\circ} = \widehat{SC,(ABCD)} = \widehat{SC,AC} = \widehat{SCA}$ .
Trong $\large \Delta SAC$, ta có h = SA = $\large a\sqrt{5}$
Ta có $\large \left\{\begin{matrix}
BC \perp AB & \\
BC \perp SA &
\end{matrix}\right.\Rightarrow BC \perp (SAB)\Rightarrow BC \perp BN$
Lại có $\large NA \perp AC$. Do đó hai điểm A, B cùng nhìn đoạn NC dưới một góc vuông nên hình chóp N.ABC nội tiếp mặt cầu tâm J là trung điểm NC, bán kính
$\large R = JN = \dfrac{NC}{2} = \dfrac{1}{2}.\sqrt{AC^{2}+\left (\frac{SA}{2} \right )^{2}} = \dfrac{5a}{4}$. Chọn A.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô
- Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc $\large \wi
- Cho tứ diện ABCD có DA vuông góc với mp( ABC ), $\large DB \perp BC$ ,
- Thể tích V của khối tròn xoay thu được khi quay hình thang ABCD quanh
- Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đườn