Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên $\lar
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=a√6 và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD ta được:
Đáp án án đúng là: B
Lời giải chi tiết:
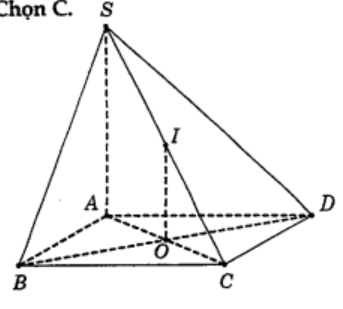
Gọi O=AC∩BD, suy ra O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Gọi I là trung điểm SC, suy ra
IO // SA ⇒IO⊥(ABCD)
Do đó IO là trục của hình vuông ABCD, suy ra IA = IB = IC = ID. (1)
Tam giác SAC vuông tại A có I là trung điểm cạnh huyền SC nên IS = IC = IA. (2)
Từ (1) và (2), ta có: R = IA = IB = IC = IS = SC2=a√2
Vậy diện tích mặt cầu S=4πR2=8πa2. Chọn B.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô
- Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc $\large \wi
- Cho tứ diện ABCD có DA vuông góc với mp( ABC ), DB⊥BC ,
- Thể tích V của khối tròn xoay thu được khi quay hình thang ABCD quanh