Cho khối lập phương $\large ABCD.A'B'C'D'$ có độ dài đường chéo $\larg

Cho khối lập phương $\large ABCD.A'B'C'D'$ có độ dài đường chéo $\large A'C=a\sqrt{3}$. Thể tích của khối lập phương đã cho bằng

• A.

  A. $\large a^{3}$

• B.

  B. $\large 3 \sqrt{3} a^{3}$

• C.

  C. $\large\frac{1}{3}a^{3}$

• D.

  D. $\large\frac{3 \sqrt{6} a^{3}}{4}$

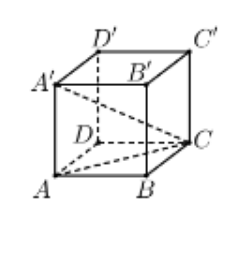
Đặt cạnh của khối lập phương là $\large x(x>0)$

Suy ra $\large AC=x\sqrt{2}$

Tam giác vuông $\large A'AC$ ta có

$\large A^{\prime} C=\sqrt{A A^{\prime 2}+A C^{2}} \Leftrightarrow a \sqrt{3}=\sqrt{x^{2}+(\sqrt{2} x)^{2}}= x \sqrt{3} \Rightarrow x=a$

Vậy thể tích khối lập phương $\large V=a^{3}$

Đáp án A