Cho khối lăng trụ đứng $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam

Cho khối lăng trụ đứng $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác cân với $\large AB=AC=a, \widehat{BAC}=120^{\circ}$. Mặt phẳng $\large (AB'C')$ tạo với đáy một góc $\large 60^{\circ}$. Thể tích của khối lăng trụ đứng bằng

• A.

  A. $\large\frac{3 a^{3}}{4}$

• B.

  B. $\large\frac{a^{3}}{8}$

• C.

  C. $\large\frac{3 a^{3}}{8}$

• D.

  D. $\large\frac{9a^{3}}{8}$

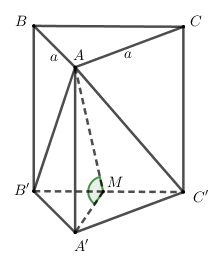
Gọi $\large M$ là trung điểm của đoạn thẳng $\large B'C'$ suy ra A'M cũng là đường cao của tam giác A'B'C'. Dễ dàng xác định được $\large 60^{\circ}=(\widehat{(AB'C'),(A'B'C'})=(\widehat{AM,A'M})=\widehat{AMA'}$

Tam giác $\large A'B'M$ ta có

$\large A^{\prime} M=A^{\prime} B^{\prime} \cdot \cos \widehat{M A^{\prime} B^{\prime}}=a \cdot \cos 60^{\circ}=\frac{a}{2}$

Tam giác vuông $\large AA'M$, có

$\large AA'=A'M \cdot \tan \widehat{AMA'}=\frac{a}{2}\cdot \tan 60^{\circ}=\frac{a\sqrt{3}}{2}$

Diện tích tam giác $\large S_{\Delta ABC}=\frac{1}{2} AB. AC \cdot \sin \widehat{B A C}=\frac{a^{2} \sqrt{3}}{4}$

Vậy thể tích khối lăng trụ $\large V_{A B C.A' B' C'}=S_{\triangle A BC} \cdot A A^{\prime}=\frac{3 a^{3}}{8}$

Đáp án C