Cho hình lăng trụ ABC.A′B′C′ có đáy là tam giác đều cạnh $\la
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình lăng trụ ABC.A′B′C′ có đáy là tam giác đều cạnh 2a√2 và AA′=a√3. Hình chiếu vuông góc của điểm A′ trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác. Thể tích của khối lăng trụ đã cho bằng
Đáp án án đúng là: A
Lời giải chi tiết:
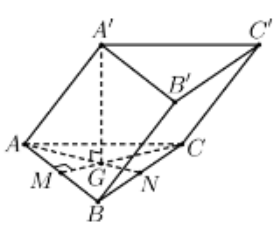
Ta có: AN=2a√2.√32=a√6 suy ra AG=23AN=23a√6
Chiều cao khối lăng trụ A′G=√A′A2−AG2=√(a√3)2−(23a√6)2=a√33
Diện tích tam giác đều SΔABC=(2a√2)2⋅√34=2a2√3
Vậy thể tích khối lăng trụ VABC.A′B′C′=SABC⋅A′G=2a3
Đáp án A