Cho khối lăng trụ đứng $\Large ABC.A'B'C'$ có đáy là tam giác vuông câ

Cho khối lăng trụ đứng $\Large ABC.A'B'C'$ có đáy là tam giác vuông cân tại $\Large C, AB=2a$ và góc tạo bởi hai mặt phẳng $\Large (ABC')$ và $\Large (ABC)$bằng $\Large 60^{\circ}$. Gọi $\Large M, N$ lần lượt là trung điểm của $\Large A'C'$ và $\Large BC$. Mặt phẳng $\Large (AMN)$ chia khối lăng trụ thành hai phần. Thể tích của phần nhỏ bằng

• A.

  $\Large \dfrac{7\sqrt{3}a^3}{24}$.

• B.

  $\Large \dfrac{\sqrt{6}a^3}{6}$.

• C.

  $\Large \dfrac{7\sqrt{6}a^3}{24}$.

• D.

  $\Large \dfrac{\sqrt{3}a^3}{3}$.

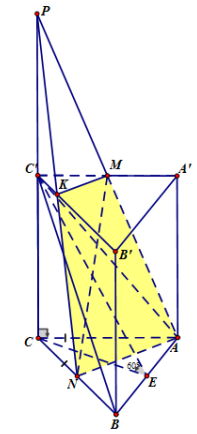
Kẻ $\Large AM$ cắt $\Large CC'$ tại $\Large P$, $\Large PN$ cắt $\Large B'C'$ tại $\Large K$. Do đó thiết diện tạo bởi mặt phẳng $\Large (AMN)$ với lăng trụ đứng $\Large ABC.A'B'C'$ là tứ giác $\Large AMKN$.

Gọi $\Large E$ là trung điểm của $\Large AB$. Khi đó góc giữa $\Large (ABC')$ và $\Large (ABC)$ là $\Large \widehat{CEC'}$ bằng $\Large 60^{\circ}$.

Ta có tam giác $\Large CAB$ vuông cân tại $\Large C$ nên $\Large CA=CB=a\sqrt{2}\Rightarrow CE=a$.

Do đó $\Large CC'=CE.\tan 60^{\circ}=a\sqrt{3}$ $\Large \Rightarrow CP=2a\sqrt{3}$, $\Large C'K=\dfrac{1}{2}CN=\dfrac{a\sqrt{2}}{4}$.

$\Large \Rightarrow V_{P.CAN}=\dfrac{1}{3}CP.\dfrac{1}{2}.AC.CN=\dfrac{a^3\sqrt{3}}{3}$ (đơn vị thể tích).

$\Large V_{P.C'MK}=\dfrac{1}{3}.C'P.\dfrac{1}{2}C'K.C'M=\dfrac{a^3\sqrt{3}}{24}$ (đơn vị thể tích).

$\Large \Rightarrow V_{CAN.C'MK}=\dfrac{7a^3\sqrt{3}}{24}$ (đơn vị thể tích).

$\Large V_{ABC.A'B'C'}=CC'.\dfrac{1}{2}AC.CB=a^3\sqrt{3}$ (đơn vị thể tích).

$\Large \Rightarrow V_{ABN.A'B'KM}$=$\Large V_{ABC.A'B'C'}-V_{ACN.MC'K}$=$\Large a^3\sqrt{3}-\dfrac{7a^3\sqrt{3}}{24}=\dfrac{17a^3\sqrt{3}}{24}$ (đơn vị thể tích).

Do đó thể tích phần nhỏ bằng $\Large V_{CAN.C'MK}=\dfrac{7a^3\sqrt{3}}{24}$ (đơn vị thể tích).