Có bao nhiêu giá trị nguyên của $\Large m$ để phương trình $\Large \ma

Có bao nhiêu giá trị nguyên của $\Large m$ để phương trình $\Large \mathrm{log}_2(mx)=\mathrm{log}_{\sqrt{2}}(x+1)$ vô nghiệm?

• A. 4.
• B. 6.
• C. 3.
• D. 5.

Xét bài toán: Tìm m để phương trình $\Large \mathrm{log}_2(mx)=\mathrm{log}_{\sqrt{2}}(x+1)$ (1) có nghiệm.

Điều kiện $\Large x+1 > 0$ (2) và $\Large mx > 0$ (3)

Với điều kiện trên thì (1) $\Large \Leftrightarrow \mathrm{log}_2(mx)=\mathrm{log}_2(x+1)^2$

$\Large \Leftrightarrow mx=(x+1)^2$ (4)

* Nếu $\Large x=0$ thì (4) vô lý.

* Nếu $\Large x\neq 0$ thì (4) $\Large \Leftrightarrow m=\dfrac{x^2+2x+1}{x}$

Xét hàm số $\Large f(x)=\dfrac{x^2+2x+1}{x}$ trên tập $\Large D=(-1; +\infty)\setminus \begin{Bmatrix} 0 \end{Bmatrix}$

$\Large f'(x)=\dfrac{x^2-1}{x^2}$

$\Large f'(x)$ không xác định tại $\Large x=0$

$\Large f'(x)=0\Leftrightarrow x=\pm 1$.

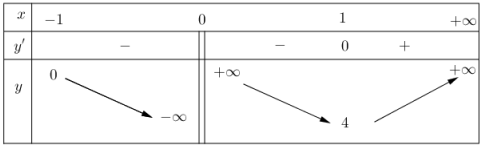
 Từ bảng biến thiên suy ra để phương trình đã cho có nghiệm thì $\Large m < 0$ hoặc $\Large m\geq 4$

Từ đó suy ra để phương trình đã cho vô nghiệm thì $\Large 0\leq m < 4$

Vậy $\Large m\in \begin{Bmatrix} 0; 1; 2; 3 \end{Bmatrix}$ thì phương trình đã cho vô nghiệm.