Cho hình lập phương $\Large ABCD.A'B'C'D'$ có cạnh bằng $\Large a$. Gọ

Cho hình lập phương $\Large ABCD.A'B'C'D'$ có cạnh bằng $\Large a$. Gọi $\Large M, N, P, Q, R, S$ là tâm các mặt của hình lập phương. Thể tích khối bát diện đều tạo bởi sáu đỉnh $\Large M, N, P, Q, R, S$ bằng

• A.

  $\Large \dfrac{a^3\sqrt{2}}{24}$.

• B.

  $\Large \dfrac{a^3}{4}$.

• C.

  $\Large \dfrac{a^3}{12}$.

• D.

  $\Large \dfrac{a^3}{6}$.

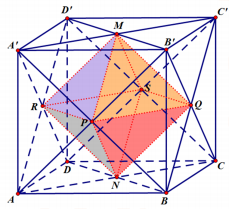
Ta có: $\Large RP$ là đường trung bình của tam giác $\Large A'BD$. Do đó: $\Large RP=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}$ và $\Large RP// BD$ (1).

$\Large PQ$ là đường trung bình của tam giác $\Large B'AC$. Do đó $\Large PQ=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}$ và $\Large PQ// AC$ (2).

$\Large QS$ là đường trung bình của tam giác $\Large B'D'C$. Do đó $\Large QS=\dfrac{1}{2}B'D'=\dfrac{a\sqrt{2}}{2}$.

$\Large SR$ là đường trung bình của tam giác $\Large A'C'D$. Do đó $\Large SR=\dfrac{1}{2}A'C'=\dfrac{a\sqrt{2}}{2}$.

Khi đó: $\Large RP=PQ=QS=SR=\dfrac{a\sqrt{2}}{2}$. Suy ra tứ giác $\Large PQSR$ là hình thoi.

Ta có: $\Large AC\perp BD$, kết hợp với (1) và (2), ta được: $\Large RP\perp QP$.

Khi đó tứ giác $\Large PQSR$ là hình vuông.

Do đó diện tích hình vuông $\Large PQSR$ là: $\Large S_{PQRS}=\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{a^2}{2}$.

Lại có: $\Large d\big(M, (PQSR)\big)=\dfrac{1}{2}DD'=\dfrac{1}{2}a$.

Thể tích khối chóp $\Large M.PQRS$ là: $\Large V_{M.PQRS}=\dfrac{1}{3}d\big(M, (PQSR)\big).S_{PQRS}=\dfrac{1}{3}.\dfrac{1}{2}a.\dfrac{a^2}{2}=\dfrac{a^3}{12}$.

Vậy thể tích khối bát diện đều tạo bởi sáu đỉnh $\Large M, N, P, Q, R, S$ là:

$\Large V_{MNPQRS}=2V_{M.PQSR}=\dfrac{a^3}{6}$.