Cho hàm số y=f(x) liên tục trên R và có đồ
Lưu về Facebook:
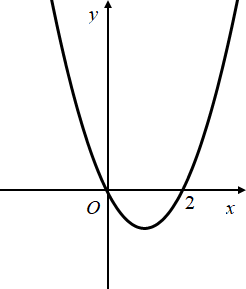
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x) liên tục trên R và có đồ thị f′(x) như hình vẽ. Số điểm cực tiểu của hàm số g(x)=f(−x2+x) là
Đáp án án đúng là: D
Lời giải chi tiết:
Ta có: g′(x)=(−2x+1)f′(−x2+x)
g′(x)=0 ⇔[−2x+1=0−x2+x=0−x2+x=2 ⇔⇔[x=12x=0x=1.
Ta thấy khi x>1 ⇒{−x2+x<0−2x+1<0 ⇒{f′(−x2+x)>0−2x+1<0 ⇒g′(x)<0.
Xét dấu g′(x) trên trục số:
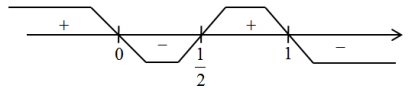
Suy ra g(x)=f(−x2+x) có 1 điểm cực tiểu.