Cho khối lăng trụ đứng $\Large ABC.A'B'C'$ có đáy là tam giác đều. Mặt

Cho khối lăng trụ đứng $\Large ABC.A'B'C'$ có đáy là tam giác đều. Mặt phẳng $\Large (A'BC)$ tạo với đáy góc $\Large 30^{\circ}$ và tam giác $\Large A'BC$ có diện tích bằng 8. Tính thể tích $\Large V$ của khối lăng trụ đã cho.

• A.

  $\Large 64\sqrt{3}$.

• B.

  $\Large 2\sqrt{3}$.

• C.

  $\Large 16\sqrt{3}$.

• D.

  $\Large 8\sqrt{3}$.

Chọn D

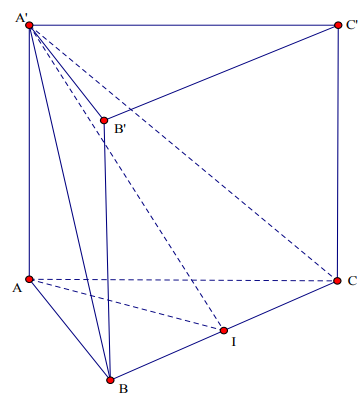
Gọi $\Large I$ là trung điểm cạnh $\Large BC$.

Vì $\Large ABC.A'B'C'$ là lăng trụ đứng có đáy là tam giác đều nên $\Large ABC.A'B'C'$ là khối lăng trụ đứng đều.

Do đó ta có: $\Large A'B=A'C$. Suy ra tam giác $\Large A'BC$ cân tại $\Large A'\Rightarrow A'I\perp BC$.

Mặt khác: tam giác $\Large ABC$ đều $\Large \Rightarrow AI\perp BC$.

Suy ra $\Large BC\perp (A'IA)$.

Vậy góc giữa mặt phẳng $\Large (A'BC)$ và mặt đáy bằng góc $\Large \widehat{A'IA}=30^{\circ}$.

Ta có: tam giác $\Large ABC$ là hình chiếu của tam giác $\Large A'BC$ trên mặt đáy nên

$\Large S_{ABC}=S_{A'BC}.cos\alpha =8.cos30^{\circ}=4\sqrt{3}$.

Đặt $\Large AB=x$ $\Large \Rightarrow S_{ABC}=\dfrac{x^2\sqrt{3}}{4}=4\sqrt{3}$ $\Large \Rightarrow x=4$.

Ta có: $\Large AI=\dfrac{x\sqrt{3}}{2}=2\sqrt{3}$ $\Large \Rightarrow AA'=AI.tan\widehat{A'IA}=2$.

Suy ra: $\Large V_{ABC.A'B'C'}=AA'.S_{ABC}=2.4\sqrt{3}=8\sqrt{3}$.