Cho khối lăng trụ đứng $\LARGE ABC.A'B'C'$ có đáy là tam giác đều cạnh

Cho khối lăng trụ đứng $\LARGE ABC.A'B'C'$ có đáy là tam giác đều cạnh $\large a$. Điểm $\large A'$ cách đều ba điểm $\large A,B,C$. Góc giữa $\large AA'$ và mặt phẳng $\large (ABC)$ bằng $\large 60^{\circ}$. Tính theo $\large a$ thể tích $\large V$ của khối lăng trụ $\large ABC.A'B'C'$

• A.

  A. $\large V=\frac{a^{3}\sqrt{3}}{12}$

• B.

  B. $\large V=\frac{a^{3}\sqrt{3}}{4}$

• C.

  C. $\large V=\frac{3a^{3}\sqrt{3}}{4}$

• D.

  D. $\large V=\frac{a^{3}\sqrt{3}}{3}$

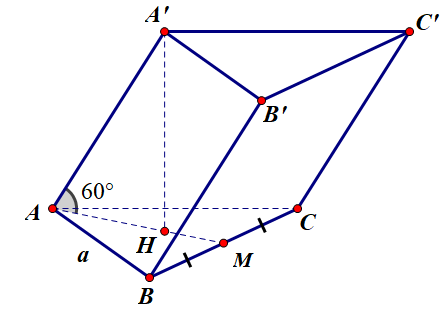
Gọi $\large H$ là trọng tâm tam giác $\large ABC$ và $\large M$ là trung điểm của $\large BC$, khi đó $\large A'.ABC$ là hình chóp đều

Suy ra $\large A'H\perp (ABC)\Rightarrow \widehat{\left ( AA';(ABC) \right )}=\widehat{A'AH}=60^{\circ}$

Tam giác $\large ABC$ đều cạnh $\large a$ nên $\large S_{ABC}=\frac{a^{2}\sqrt{3}}{4}$ và $\large AM=\frac{a\sqrt{3}}{2}\Rightarrow AH=\frac{2}{3}AM=\frac{a\sqrt{3}}{3}$

$\large\Rightarrow A'H=AH\tan \widehat{A'AH}=\frac{a\sqrt{3}}{3}\tan 60^{\circ}=a$

Khi đó $\large V=A'H\cdot S_{ABC}=a\cdot \frac{a^{2}\sqrt{3}}{4}=\frac{a^{3}\sqrt{3}}{4}$

Đáp án B