Cho hình chóp $\large S.ABCD$ có đáy là hình thoi cạnh bằng 1, góc $\l

Cho hình chóp $\large S.ABCD$ có đáy là hình thoi cạnh bằng 1, góc $\large\widehat{ABC}=60^{\circ}$. Cạnh bên $\large SD=\sqrt{2}$ Hình chiếu vuông góc của $\large S$ trên mặt phẳng $\large (ABCD)$ là điểm $\large H$ thuộc đoạn $\large BD$ thỏa mãn $\large HD=3HB$. Thể tích khối chóp đã cho bằng.

• A.

  A. $\large\frac{\sqrt{15}}{8}$

• B.

  B. $\large\frac{\sqrt{15}}{12}$

• C.

  C. $\large\frac{\sqrt{5}}{24}$

• D.

  D. $\large\frac{\sqrt{15}}{24}$

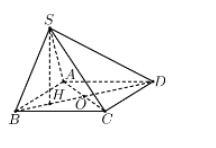
Vì $\large\widehat{ABC}=60^{\circ}$ nên tam giác $\large ABC$ đều

Suy ra $\large BO=\frac{\sqrt{3}}{2};BD=2BO=\sqrt{3};HD=\frac{3}{4}BD=\frac{3\sqrt{3}}{4}$

Tam giác vuông $\large SHD$, có $\large SH=\sqrt{SD^{2}-HD^{2}}=\frac{\sqrt{5}}{4}$

Diện tích hình thoi $\large S_{ABCD}=2S_{\bigtriangleup ABC}=\frac{\sqrt{3}}{2}$

Thể tích khối chóp $\large V_{S.ABCD}=\frac{1}{3}S_{ABCD}.SH=\frac{\sqrt{15}}{24}$

Đáp án D