Cho hình chóp S.ABCD có đáy là hình thang cân với cạnh đáy $\
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thang cân với cạnh đáy AD và BC,AD=2a,AB=BC=CD=a. Cạnh bên SA vuông góc với mặt phẳng đáy và SD tạo với mặt phẳng đáy góc 45∘. Thể tích của khối chóp đã cho bằng
Đáp án án đúng là: B
Lời giải chi tiết:
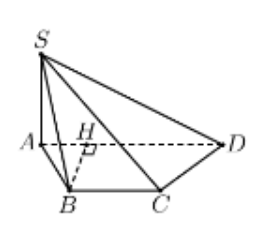
Xác định 45∘=(^SD,(ABCD))=(^SD,AD)=^SDA
Chiều cao khối chóp SA=AD⋅tan^SDA=2a
Ta thấy hình thang cân đã cho là nửa lục giác đều có cạnh bằng a nên có diện tích SABCD=3×a2√34
Vậy thể tích khối chóp VS.ABCD=13SABCD.SA=a3√32
Đáp án B
Xem thêm các bài tiếp theo bên dưới