Cho hình chóp S.ABCDS.ABCD có đáy là hình vuông cạnh aa. Cạ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCDS.ABCD có đáy là hình vuông cạnh aa. Cạnh bên SASA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD)(SBD) và mặt phẳng đáy bằng 60∘60∘. Thể tích của khối chóp đã cho bằng
Đáp án án đúng là: C
Lời giải chi tiết:
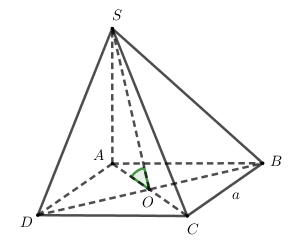
Xác định 60∘=(^(SBD),(ABCD))=(^SO,AO)=^SOA60∘=(ˆ(SBD),(ABCD))=(ˆSO,AO)=ˆSOA
Ta có: AO=12AC=12.a√2=a√22AO=12AC=12.a√2=a√22
Chiều cao khối chóp SA=AO⋅tan^SOA=a√62SA=AO⋅tanˆSOA=a√62
Diện tích hình vuông SABCD=a2SABCD=a2
Vậy thể tích khối chóp VS.ABCD=13SABCD.SA=a3√66VS.ABCD=13SABCD.SA=a3√66
Đáp án C
Xem thêm các bài tiếp theo bên dưới