Cho hình chóp $\large S.ABCD$ có đáy là hình thoi cạnh $\large a$, đườ

Cho hình chóp $\large S.ABCD$ có đáy là hình thoi cạnh $\large a$, đường chéo $\large AC=a$. Tam giác $\large SAB$  cân tại $\large S$ và nằm trong mặt phẳng vuông góc với mặt đáy, góc giữa $\large (SCD)$ và mặt đáy bằng $\large 45^{\circ}$. Thể tích của khối chóp đã cho bằng.

• A.

  A. $\large\frac{a^{3}}{2}$

• B.

  B. $\large\frac{a^{3}}{4}$

• C.

  C. $\large\frac{3a^{3}}{4}$

• D.

  D. $\large\frac{a^{3}}{12}$

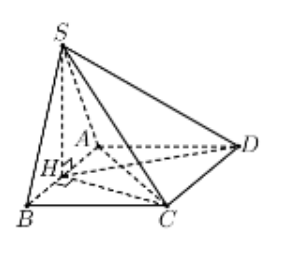
Gọi $\large H$ là trung điểm $\large AB$

Từ giả thiết suy ra $\large SH\perp (ABCD)$

Ta có ABCD là hình thoi cạnh a mà AC = a, suy ra ABC và ACD là  hai tam giác đều cạnh a $\large \Rightarrow HC=\frac{a\sqrt{3}}{2}$

$\large \Rightarrow \widehat{HCD}=\widehat{HAC}+\widehat{ACD}=30^{0}+60^{0}=90^{0}\Rightarrow HC\perp CD$

Xác định $\large 45^{\circ}=(\widehat{(SCD),(A B C D)})=(\widehat{SC,HC})=\widehat{SCH}$

Chiều cao khối chóp $\large SH=HC\cdot\tan\widehat{SCH}=\frac{a \sqrt{3}}{2}$

Diện tích hình thoi $\large S_{ABCD}=2S_{\Delta ABC}=\frac{a^{2} \sqrt{3}}{2}$

Vậy thể tích khối chóp $\large V_{S.ABCD}=\frac{1}{3} S_{ABCD}. SH=\frac{a^{3}}{4}$

Đáp án B