Cho hình vuông $\Large A_1B_1C_1D_1$ có cạnh bằng 1. Gọi $\Large A_{k+

Cho hình vuông $\Large A_1B_1C_1D_1$ có cạnh bằng 1. Gọi $\Large A_{k+1}, B_{k+1}, C_{k+1}, D_{k+1}$ theo thứ tự là trung điểm của các đoạn thẳng $\Large A_kB_k, B_kC_k, C_kD_k, D_kA_k$ (với $\Large k=1, 2,..$). Chu vi của hình vuông $\Large A_{2018}B_{2018}C_{2018}D_{2018}$ bằng

• A.

  $\Large \dfrac{\sqrt{2}}{2^{2019}}$.

• B.

  $\Large \dfrac{\sqrt{2}}{2^{1006}}$.

• C.

  $\Large \dfrac{\sqrt{2}}{2^{2018}}$.

• D.

  $\Large \dfrac{\sqrt{2}}{2^{1007}}$.

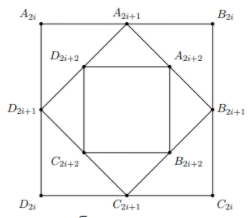
Gọi $\Large u_i$ là chu vi của hình vuông $\Large A_{2i}B_{2i}C_{2i}D_{2i}$.

Dễ thấy $\Large A_{2i+2}D_{2i+2}=\dfrac{1}{2}A_{2i}B_{2i}$, từ đó chu vi hình vuông $\Large A_{2i+2}B_{2i+2}C_{2i+2}D_{2i+2}$ bằng 2 lần chu vi hình vuông $\Large A_{2i}B_{2i}C_{2i}D_{2i}$ nên $\Large u_{i+1}=\dfrac{1}{2}u_i$.

Ngoài ra $\Large A_2B_2=\sqrt{2}A_2B_1=\dfrac{\sqrt{2}}{2}$ nên $\Large u_1=2\sqrt{2}$.

Dãy số $\Large (u_n)$ là cấp số nhân có công bội $\Large \dfrac{1}{2}$ nên $\Large u_n=\left(\dfrac{1}{2}\right)^{n-1}=2\sqrt{2}.\dfrac{1}{2^{n-1}}=\dfrac{\sqrt{2}}{2^{n-2}}$.

Do đó chu vi của hình vuông $\Large A_{2018}B_{2018}C_{2018}D_{2018}$ bằng $\Large u_{1009}=\dfrac{\sqrt{2}}{2^{1007}}$.

Chọn đáp án D.