Cho hình trụ $\Large (T)$ được sinh ra khi quay hình chữ nhật $\Large

Cho hình trụ $\Large (T)$ được sinh ra khi quay hình chữ nhật $\Large ABCD$ quanh cạnh $\Large AB$. Biết $\Large AC=2\sqrt{2}a$ và $\Large \widehat{ACB}=45^{o}$. Diện tích toàn phần của hình trụ $\Large (T)$ bằng

• A.

  A. $\large 16\pi a^{2}$

• B.

  B. $\large 10\pi a^{2}$

• C.

  C. $\large 12\pi a^{2}$

• D.

  D. $\large 8\pi a^{2}$

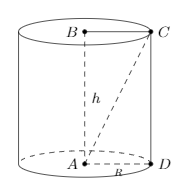
Xét tam giác ABC vuông tại B, $\large \widehat{ACB}=45^{o}, AC=2\sqrt{2}a\Rightarrow AB=AC \sin 45^{o}=2a$

Ta có: $\large h=AB=2a, R=BC=AC \cos 45^{o}=2a$

Ta có diện tích xung quanh của hình trụ (T) là: $\large S_{xq}=2\pi Rh=2\pi .2a.2a=8\pi a^{2}$

Diện tích một mặt đáy là: $\large \pi R^{2}=4\pi a^{2}$

Diện tích toàn phần của hình trụ là: $\large S_{tp}=S_{xq}+2S_{d}=8\pi a^{2}+2.4\pi a^{2}=16\pi a^{2}$

Chọn đáp án A.