Cho hình cầu tâm O bán kính R = 5, tiếp xúc với mặt phẳng ( P ). Một h
MỤC LỤC
Câu hỏi:
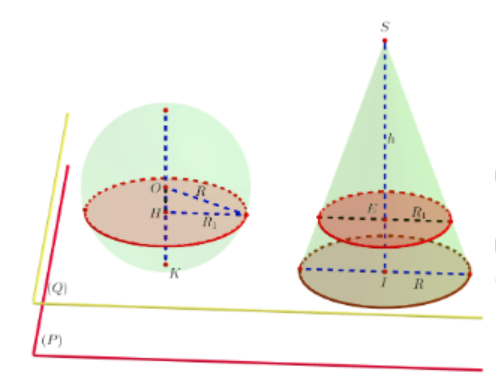
Cho hình cầu tâm O bán kính R = 5, tiếp xúc với mặt phẳng (P). Một hình nón tròn xoay có đáy nằm trên (P), có chiều cao h = 15, có bán kính đáy bằng R. Hình cầu và hình nón nằm về một phía đối với mặt phẳng (P). Người ta cắt hai hình đó bởi mặt phẳng (Q) song song với (P) và thu được hai thiết diện có tổng diện tích là S. Gọi x là khoảng cách giữa (P) và (Q), $\large (0

Đáp án án đúng là: B
Lời giải chi tiết:
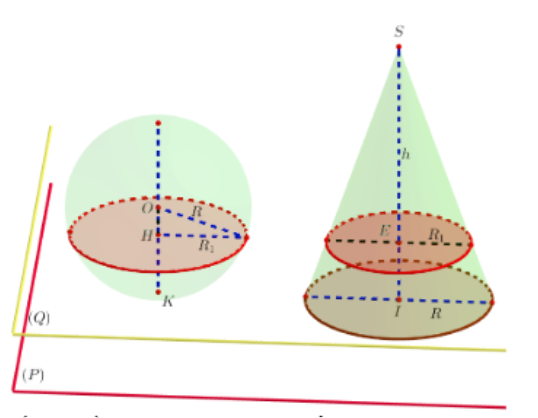
Nhận thấy khi ta cắt hình cầu và hình nón bởi mặt phẳng (Q) song song với (P) thì hai thiết diện đều là hình tròn.
Gọi $\large R_{2}, R_{1}$ lần lượt là bán kính, còn H, E lần lượt là tâm của hai hình tròn thiết diện đó.
Gọi K là tiếp điểm của mặt cầu với (P), còn I là tâm mặt đáy của hình nón.
Theo giả thiết HK = EI = x, $\large 0
Ta có: $\large R_{2}^{2}= R^{2}-OH^{2}= R^{2}-(5-x)^{2}= 10x-x^{2}$.
$\large \dfrac{R_{1}}{R}= \dfrac{SE}{SI}= \dfrac{15-x}{15}\Rightarrow R_{1}= \dfrac{15-x}{3}$.
Do đó:
$\large S = \pi R_{1}^{2}+\pi R_{2}^{2}= \pi(10x-x^{2})+\pi \left (\dfrac{15-x}{3} \right )^{2}= \dfrac{\pi }{9}(-8x^{2}+60x+225)$
$\large S = \dfrac{75\pi }{2}-\dfrac{8\pi }{9}\left (x-\dfrac{15}{4} \right )^{2}\leq \dfrac{75\pi }{2}$
Đẳng thức xảy ra khi và chỉ khi $\large x = \dfrac{15}{4}$.
S đạt giá trị lớn nhất khi $\large x = \dfrac{a}{b} = \dfrac{15}{4}$. Vậy T = a+b = 19.
Xem thêm các bài tiếp theo bên dưới
- Bất phương trình $\Large 4^x-(m+1).2^{x+1}+m\geq0$ nghiệm đúng với mọi
- Có bao nhiêu giá trị thực của $\Large m$ để bất phương trình $\Large 4
- Tìm hệ số của số hạng chứa $\Large x^8$ trong khai triển nhị thức Newt
- Có 6 học sinh và 3 thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế
- Biết n à số nguyên dương thỏa mãn $\Large C _{n}^{n-1}+ C _{n}^{n-2}=7