Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\Large AB = A

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\Large AB = AC = a$. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc $\large 60^{\circ}$. Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số $\large \dfrac{V}{S}$ bằng?

• A.

  A. $\large a\sqrt{14}$

• B.

  B. $\large \dfrac{a\sqrt{14}}{12}$

• C.

  C. $\large \dfrac{3a\sqrt{14}}{4}$

• D.

  D. $\large \dfrac{a\sqrt{2}}{6}$

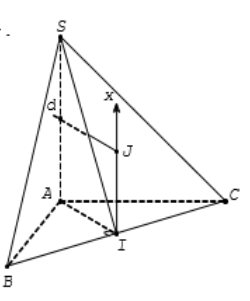
Ta có $\large 60^{\circ} = (\widehat{SI,(ABC)}) = (\widehat{SI,AI}) = \widehat{SIA}$.

Tam giác ABC vuông cân tại A, suy ra $\large AI = \dfrac{1}{2}BC = \dfrac{a\sqrt{2}}{2}$.

Trong $\large \triangle SAI$, ta có $\large SA = AI. \tan \widehat{SIA}= \dfrac{a\sqrt{6}}{2}$.

Kẻ Ix $\large \perp$ (ABC)  (như hình vẽ)

Suy ra Ix là trục của $\large \triangle$ABC.

Trong mặt phẳng (SA,Ix), kẻ trung trực d của đoạn thẳng SA cắt Ix tại J. Khi đó J chính là tâm mặt cầu ngoại tiếp hình chóp.

Bán kính: $\large R = JA = \sqrt{JI^{2}+AI^{2}} = \dfrac{a\sqrt{14}}{4}$ nên

$\large \dfrac{V}{S} = \dfrac{R}{3} = \dfrac{a\sqrt{14}}{12}$. Chọn B.