Cho hình phẳng giới hạn bởi đồ thị các hàm số $\Large y=\sqrt{x}$, đườ
Lưu về Facebook:
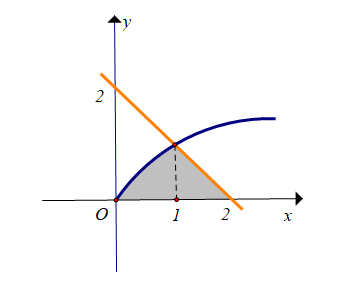
MỤC LỤC
Câu hỏi:
Cho hình phẳng giới hạn bởi đồ thị các hàm số $\Large y=\sqrt{x}$, đường thẳng $\Large y=2-x$ và trục hoành ( phần tô màu trong hình vẽ). Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục $\Large Ox$ bằng
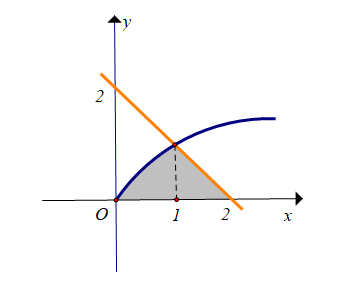
Đáp án án đúng là: D
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm $\Large \sqrt{x}=2-x\Leftrightarrow x=1$
Thể tích của khối tròn xoay sinh bởi hình phẳng đã cho khi quay quanh trục $\Large Ox$ là
$\Large \begin{align}& V_{Ox}=\pi\int_{0}^{1}\sqrt{x}^2dx+\pi\int_{1}^{2}(2-x)^2dx=\pi\int_{0}^{1} x dx+\pi\int_{1}^{2}(x^2-4x+4)dx\\&=\pi\left[\dfrac{x^2}{2}\bigg|_0^1 +\left( \dfrac{{{x}^{3}}}{3}-2{{x}^{2}}+4x \right)\bigg|_1^2\right]=\dfrac{5\pi}{6}\end{align}$
Chọn đáp án D
Xem thêm các bài tiếp theo bên dưới
- Thể tích $\Large V$ của vật tròn xoay tạo thành khi quay hình phẳng $\
- Độ lớn của vận tốc của một vật thay đổi theo thời gian $\Large v=f(t)$
- Thể tích khối tròn xoay sinh ra khi quay trục $\Large Ox$ hình phẳng g
- Trong mặt phẳng tọa độ Oxy , gọi $\Large (H1)$ là hình phẳng giới hạn
- Diện tích hình phẳng phần gạch chéo trong hình vẽ bên được tính theo c