Trong mặt phẳng tọa độ Oxy , gọi $\Large (H1)$ là hình phẳng giới hạn

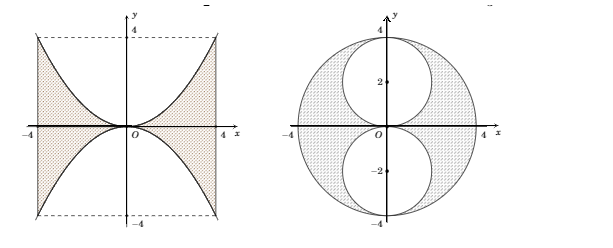
Trong mặt phẳng tọa độ Oxy , gọi $\Large (H1)$ là hình phẳng giới hạn bởi các đường $\Large y=\dfrac{{{x}^{2}}}{4},y=-\dfrac{{{x}^{2}}}{4}$,$\Large x=-4,x=4$ và $\Large (H2)$ là hình gồm các điểm $\Large (x;y)$ thỏa mãn $\Large {{x}^{2}}+{{y}^{2}}\le 16,{{x}^{2}}+{{(y-2)}^{2}}\ge 4,{{x}^{2}}+{{(y+2)}^{2}}\ge 4$ . Cho $\Large (H1)$ và $\Large (H2)$ quay quanh trục $\Large Oy$ ta được các vật thể có thể tích lần lượt là $\Large {{V}_{1}},{{V}_{2}}$. Đẳng thức nào sau đây đúng?

• A.

  $\Large {{V}_{1}}={{V}_{2}}$

• B.

  $\Large {{V}_{1}}=\dfrac{1}{2}{{V}_{2}}$

• C.

  $\Large {{V}_{1}}=2{{V}_{2}}$

• D.

  $\Large {{V}_{1}}=\dfrac{2}{3}{{V}_{2}}$

- Tính thể tích $\Large V_1$.

+ Thể tích khối trụ bán kính $\Large r=4$, chiều cao $\Large h=8$ là $\Large V=\pi r^2h=128\pi$.

+ $\Large y=\dfrac{x^2}{4} \Rightarrow x^2 = 4y\Rightarrow x=2\sqrt {y}$ với $\Large x\geq 0$. Thể tích giới hạn bởi parabol $\Large y=\dfrac{x^2}{4}$, trục tung, đường thẳng $\Large y=4$ quanh trục $\Large Oy$ là :

$\Large V_{(P)}=\pi\int_{0}^{4} x^2dy=\pi\int_{0}^{4}4ydy=32\pi$

Suy ra thể tích sinh bởi $\Large \left(H_1\right)$ là

$\Large V_1=V - 2.V_{(P)}=128\pi - 2.32\pi=\64 \pi$

- Tính thể tích $\Large V_2$

+ Thể tích khồi cấu bán kính $\Large R=4$ là $\Large V_L=\dfrac{4}{3}\pi R^3=\dfrac{256}{3}\pi.$

+ Thể tích khối cầu bán kính $\Large r=2$ là $\Large V_N=\dfrac{4}{3}\pi r^3=\dfrac{32}{3}\pi.$

Suy ra thể tích sinh bởi $\Large H_2$ là:

$\Large V_2=V_L-2V_N=\dfrac{256}{3}\pi-\dfrac{2. 32}{3}\pi=64 \pi.$

Vậy $\Large V_1=V_2$

Đáp án đúng: A