Cho hình nón đỉnh S , đường cao SO . Gọi A, B là hai điểm thuộc đường

Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và $\large \widehat{SAO} = 30^{\circ}$, $\large \widehat{SAB} = 60^{\circ}$. Độ dài đường sinh l của hình nón bằng:

• A.

  A. l = a

• B.

  B. $\large l = a\sqrt{2}$

• C.

  C. $\large l = a\sqrt{3}$

• D.

  D. l = 2a

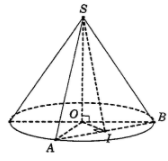
Gọi I là trung điểm AB, suy ra $\large OI \perp AB$, $\large SI \perp AB$ và OI = a.

Trong tam giác vuông SOA, ta có $\large OA = SA.cos\widehat{SAO} = \dfrac{SA\sqrt{3}}{2}$ 

Trong tam giác vuông SIA, ta có $\large IA = SA.cos\widehat{SAB} = \dfrac{SA}{2}$ 

Trong tam giác vuông OIA, ta có

$\large OA^{2} = OI^{2}+IA^{2}\Leftrightarrow \dfrac{3}{4}SA^{2} = a^{2}+\dfrac{1}{4}SA^{2}\Rightarrow SA = a\sqrt{2}$ 

Chọn B.