Cho hình nón đỉnh S, đáy là hình tròn tâm O, độ dài đường sinh bằng 2a

Cho hình nón đỉnh S, đáy là hình tròn tâm O, độ dài đường sinh bằng 2a. Một mặt phẳng đi qua đỉnh S cắt hình nón theo thiết diện là tam giác SAB có diện tích lớn nhất. Biết khoảng cách từ O đến đường thẳng AB bằng a. Thể tích khối nón tạo bởi hình nón trên bằng

• A. A. $\Large 4\pi a^{3}$
• B. B. $\Large \pi a^{3}$
• C. C. $\Large 3\pi a^{3}$
• D. D. $\Large \dfrac{4\pi a^{3}}{3}$

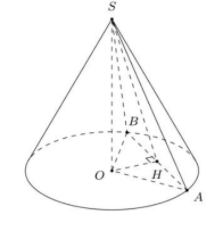
Ta có độ dài đường sinh $\Large l = 2a, OH = a$

Tam giác SAB cân tại S. Diện tích tam giác ABC là

$\Large S_{\Delta SAB} = \dfrac{1}{2}SA.SB.\sin\widehat{ASB} = \dfrac{1}{2}l^{2}.\sin\widehat{ASB} \leq \dfrac{l^{2}}{2}$

Do đó, diện tích tam giác SAB lớn nhất khi $\Large \sin\widehat{ASB} = 1$ hay tam giác SAB vuông cân tại S

Khi đó $\Large AB = \sqrt{SA^{2}+SB^{2}} = \sqrt{2l^{2}} = 2\sqrt{2}a$

Bán kính đáy $\Large r = \sqrt{OH^{2}+HA^{2}} = \sqrt{OH^{2} + \dfrac{AB^{2}}{4}} = \sqrt{a^{2}+2a^{2}} = a\sqrt{3}$

Chiều cao của hình nón $\Large h = \sqrt{l^{2}-r^{2}} = a$

Thể tích khối nón là $\Large V = \dfrac{1}{3} \pi r^{2}h = \dfrac{1}{3}\pi.3a^{2}.a = \pi a^{3}$