Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm các cạnh AB và AD, H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH=a√3SH=a√3. Tính khoảng cách giữa hai đường thẳng DM và SC
Đáp án án đúng là: A
Lời giải chi tiết:
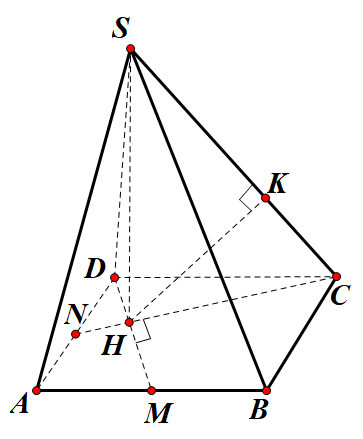
Vì ΔMAD=ΔNDCΔMAD=ΔNDC nên ^ADM=^DCNˆADM=ˆDCN suy ra MD⊥NCMD⊥NC
Ta có DM⊥NC,DM⊥SHDM⊥NC,DM⊥SH nên DM⊥(SHC)DM⊥(SHC), suy ra DM⊥SCDM⊥SC
Kẻ HK⊥SC,(K∈(SC)HK⊥SC,(K∈(SC). Suy ra HK là đoạn vuông góc chung của DM và SC nên d(DM,SC) = HK
Ta có HC=CD2CN=2a√5HC=CD2CN=2a√5 và HK=SH.HC√SH2+HC2=2√57a19HK=SH.HC√SH2+HC2=2√57a19
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số f(x)f(x) có bảng biến thiên như sau: Số giá trị nguyên
- Cho hàm số y=f(x)y=f(x) có đạo hàm trên R và $\
- Một hộp chứa 15 cái thẻ được đánh số từ 1 đến 15, rút ngẫu nhiên ba cá
- Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn $\Large \log_3(
- Anh A vào làm ở công ty X với mức lương ban đầu 10 triệu đồng/tháng. N